De database
De database achter deze toepassing bestaat uit twee tabellen: een tabel met de brongegevens van de opgave en een tabel waarin de inhoud van de matrix (9 bij 9 cellen) vastgelegd wordt. Elke cel van de matrix wordt ge´dentificeerd door het nummer van de opgave, het rijnummer en het kolomnummer.Oplossen
Het oplossen van een opgave verloopt, afhankelijk van de moeilijkheidsgraad, in een of twee fases. Hieronder beschrijf ik wat er in die fases gebeurt.Fase 1
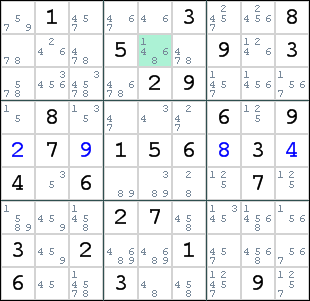
In de eerste fase pas ik een aantal methodes toe voor het wegstrepen van mogelijkheden bij nog niet ingevulde cellen en voor het vinden van oplossingen voor de lege cellen. De methodes zijn:- Het wegstrepen van opties op basis van ingevulde cellen. Als bijvoorbeeld ergens in een cel de waarde 2 staat is de 2 voor de andere cellen in die rij, in die kolom en in dat blok (3 bij 3 cellen) geen mogelijkheid meer. Hiermee kunnen ook unieke oplossingen voor cellen gevonden worden. In het volgende voorbeeld blijkt na wegstrepen van de opties dat in cel R5K3 alleen de 9 nog als optie resteert.
- Nagaan of in drie naast elkaar gelegen kolommen (1/2/3, 4/5/6 en 7/8/9) bepaalde waardes in twee van die kolommen zijn ingevuld (de waarde staat dan per definitie ook in twee verschillende blokken). Als dat zo is moet die waarde in de andere kolom in het andere blok komen. Indien de waarde maar in 1 cel van dat blok geplaatst kan worden, is de oplossing voor die cel gevonden. In de opgave hieronder moet in kolom 5 in blok 2 een 1 geplaatst worden. Dat kan vanwege de 1 in R1K2 alleen in R2K5: oplossingen gevonden.
- Als een in een blok ontbrekende waarde maar in 1 rij of kolom binnen dat blok een optie is, kan je die waarde in de rest van de rij of kolom (in de andere blokken) als optie schrappen. Dit reduceert wederom het aantal mogelijkheden en levert eventueel ook unieke oplossingen voor cellen op. In onderstaande opgave kan de 1 in blok 2 alleen in kolom 4 geplaatst worden en moet dus in een van de twee cellen (R1K4 of R3K4) komen. De optie 1 kan in de rest van kolom 4 geschrapt worden.
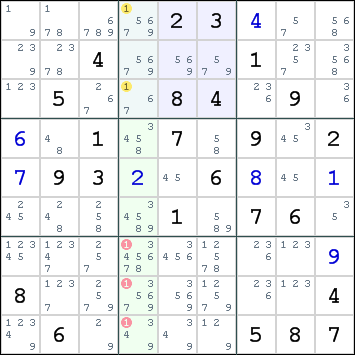
Een variant van deze methode is dat indien een bepaald cijfer in een kolom of rij maar in 1 blok een optie is, dat cijfer als optie in de rest van het blok weggestreept kan worden. In het voorbeeld kan de 2 in kolom 7 alleen in blok 9 geplaatst worden. De 2 vervalt daarmee als optie voor de overige cellen in dat blok. - Nagaan of een ontbrekende waarde nog maar in 1 cel binnen een rij, kolom of blok een optie is. Zo ja, dan is weer een oplossing gevonden. In onderstaand voorbeeld kan in kolom 5 de 1 uitsluitend nog in cel R2K5 geplaatst worden.
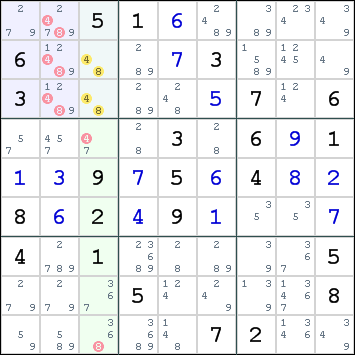
- Een volgende methode is die van de naked pairs. Klinkt spannend, maar komt gewoon op het volgende neer. Als er in een rij of kolom binnen een blok twee cellen zijn waar uitsluitend dezelfde twee cijfers een optie zijn, kunnen die cijfers in de rest van die rij of kolom en dat blok weggestreept worden. In onderstaand voorbeeld moeten de 4 en de 8 in blok 1 in kolom 3 terecht komen. Daarmee kunnen die waardes als optie in de rest van het blok en de kolom geschrapt worden.
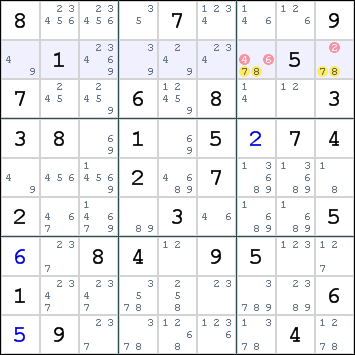
- De paren kunnen ook verborgen zijn; er is dan sprake van hidden pairs. In onderstaand voorbeeld zijn in rij 2 de waardes 7 en 8 alleen in de kolommen 7 en 9 een optie. De 7 en de 8 moeten dus in R2K7 en R2K9 komen. Dat betekent ook dat de overige waardes in die cellen als optie weggestreept kunnen worden.
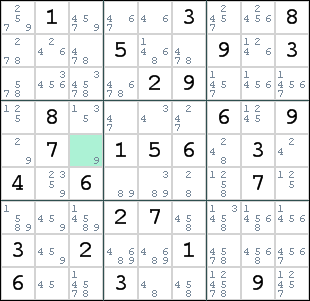
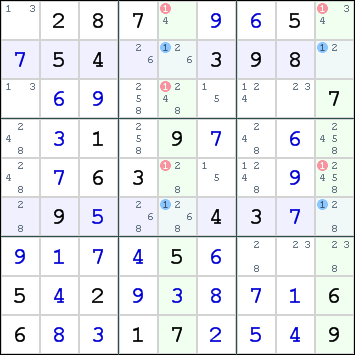
- De (vooralsnog) laatste methode die ik toepas is de zogenaamde X-wing. In het voorbeeld hieronder zie je dat op rij 2 en op rij 6 de waarde 1 alleen in de kolommen 5 en 9 een optie is (blauwe rondjes). Dat houdt in dat de 1 in beide kolommen op een van de rijen moet komen. De 1 kan daardoor als optie geschrapt worden in de andere rijen in de kolommen 5 en 9 (rode rondjes).
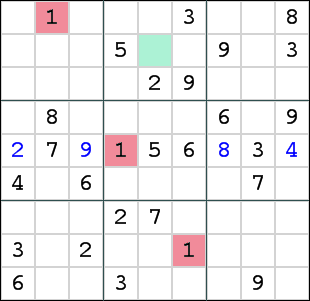
Hetzelfde principe werkt voor naast elkaar gelegen rijen.
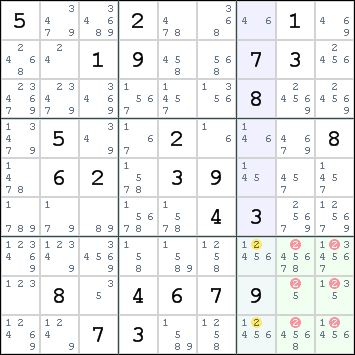
De methodes worden herhaald doorlopen totdat de opgave opgelost is of er geen opties meer weggestreept kunnen worden. Is de opgave niet volledig opgelost, dan treedt fase 2 in werking. Uiteraard wordt in elke methode waar nodig rekening gehouden met de specifieke kenmerken van sudoku-variant in kwestie.
Fase 2
In de eventuele tweede fase gooien we er (gedoseerd) wat brute kracht tegenaan.Van alle nog openstaande cellen verzamel ik de waardes die nog mogelijk zijn in die cellen. In deze fase probeer ik steeds combinaties van twee mogelijkheden uit door ze als oplossing in de opgave te zetten. Stel: in cel 1/3 zijn de waardes 3 en 8 nog mogelijk en in cel 6/8 kunnen de 2 en de 6 nog geplaatst worden. Ik vul dan bijvoorbeeld de 3 in cel 1/3 in en de 6 in cel 6/8. Daarna laat ik de methodes van fase 1 er op los. Resulteert dat in een compleet opgeloste opgave, dan zijn we klaar. Zo niet, dan probeer ik het met een volgende combinatie. Enzovoort, enzovoort......
Deze methode werkt het snelst als je hem toepast op cellen waarvoor er nog maar een beperkt aantal mogelijkheden is. Daarom sorteer in de opstaande cellen in oplopende volgorde van het aantal mogelijke opties. Cellen waar nog maar twee opties over zijn komen dus het eerst aan bod.
Als zelfs het doorrekenen van alle combinaties van mogelijke opties geen resultaat oplevert, is de opgave voor het algoritme onoplosbaar. Uiteraard sta ik altijd open voor suggesties om de effectiviteit en de performance te verbeteren.